[無料ダウンロード！ √] 平方根 因数 分解 257564

根号表

平方の公式 展開の公式があと \(2\) つありました。 それ対応する因数分解が当然 \(2\) つあります。 まずは平方の公式です。 因数分解の公式が使えない とか、 共通因数でくくれない って問題だと思うんだ。 そんなときに助けてくれるのが、 たすき掛けの因数分解 だ。 たすき（襷）といえば、 駅伝とか、 宴会の余興をイメージしちゃうかもね。 だけど、因数分解にもじつは、

平方根 因数 分解

平方根 因数 分解- 平方根も因数分解もできないなら 解の公式！ \ (x^28x4=0\)、\ (2x^26x3=0\) など。 それぞれの解き方を何度も練習して自分のモノにしてください！ このページでは、中学3年生の数学で押さえておきたい重要ポイントである "多項式の計算" 、 "因数分解平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の

算法设计与分析 二 知乎

 平方根とは 「aという数字を2乗した数がbである」この時に「aはbの平方根である」 と言い表すことが出来ます。 実際に数字を入れてみましょう。 「4の平方根は2と2である」と言い表すことが出来ます。 通常は±2という符号を使うことになります。 平方根を求めるときの考え方を学んだんじゃ 平方根を求める手順は、以下だったわけじゃ (1)、\( ± \sqrt{} \) をつける (2)、平方根の中の数字が小さくなるか、素因数分解をして調べる (31)、小さくならないなら、そのまま答えにするPocket 今回は、中3で学習する二次方程式の単元から 平方根の考え方を利用して計算する方法 について解説していくよ！ 二次方程式の解き方は、大きく分けて4パターンあります。 平方根の考えを利用して解く ⇐ 今回の記事 因数分解を利用して解く 解

 この式を因数分解すると と、なります。 この時、右辺をにするためには、左辺の(x2)か(x4)を0にすれば、成り立ちます。 ですので、x2=0と、x4=0の両方を考えれば良い事になります。 ここまで来れば簡単ですね？ x=2とx=4が正解となります。 平方根を使っ平方根の利用 パワーポイント教材(1057k) ワークシートパック 二次方程式の導入 パワーポイント教材(5104k) 指導案：word10 本時の流れはスライド1、板書計画は最後のスライドに入れています。 素因数分解でルートを外す 平方根の公式 を使って、平方因数をルートの外に出す。 実際に数字を入れて確認すると分かりやすい。 (1) (2) (3) こんな感じ。 定義を知る 細かい言葉にも細かい意味がある。 まとめ 素因数分解ができれば確実に計算がはかどる。

平方根 因数 分解のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
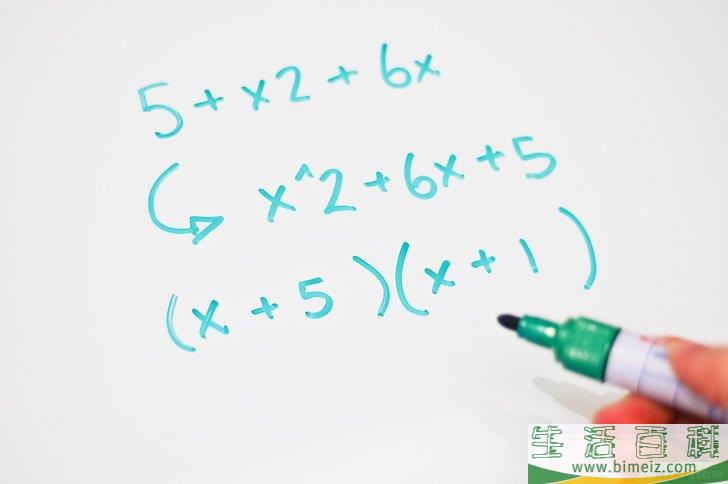平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	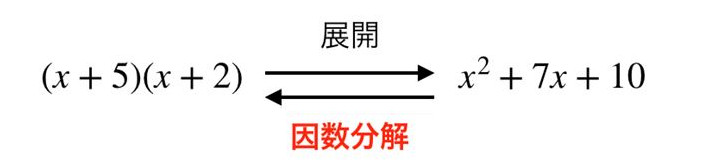平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	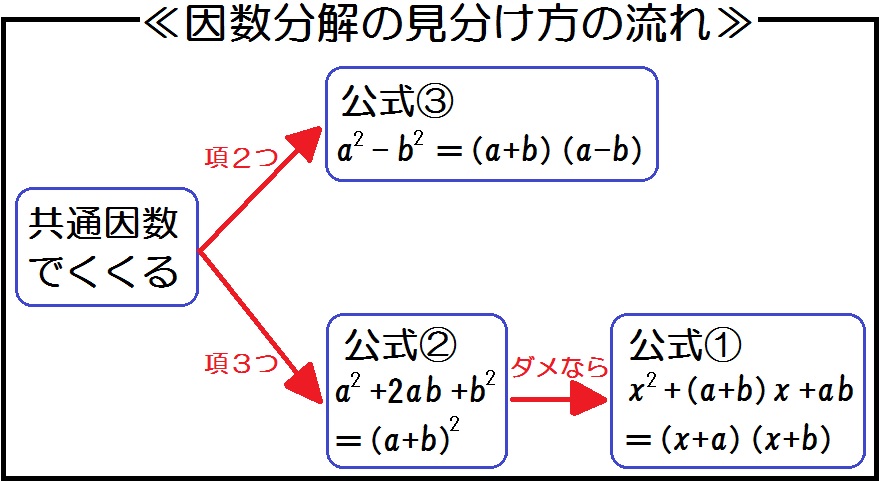平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	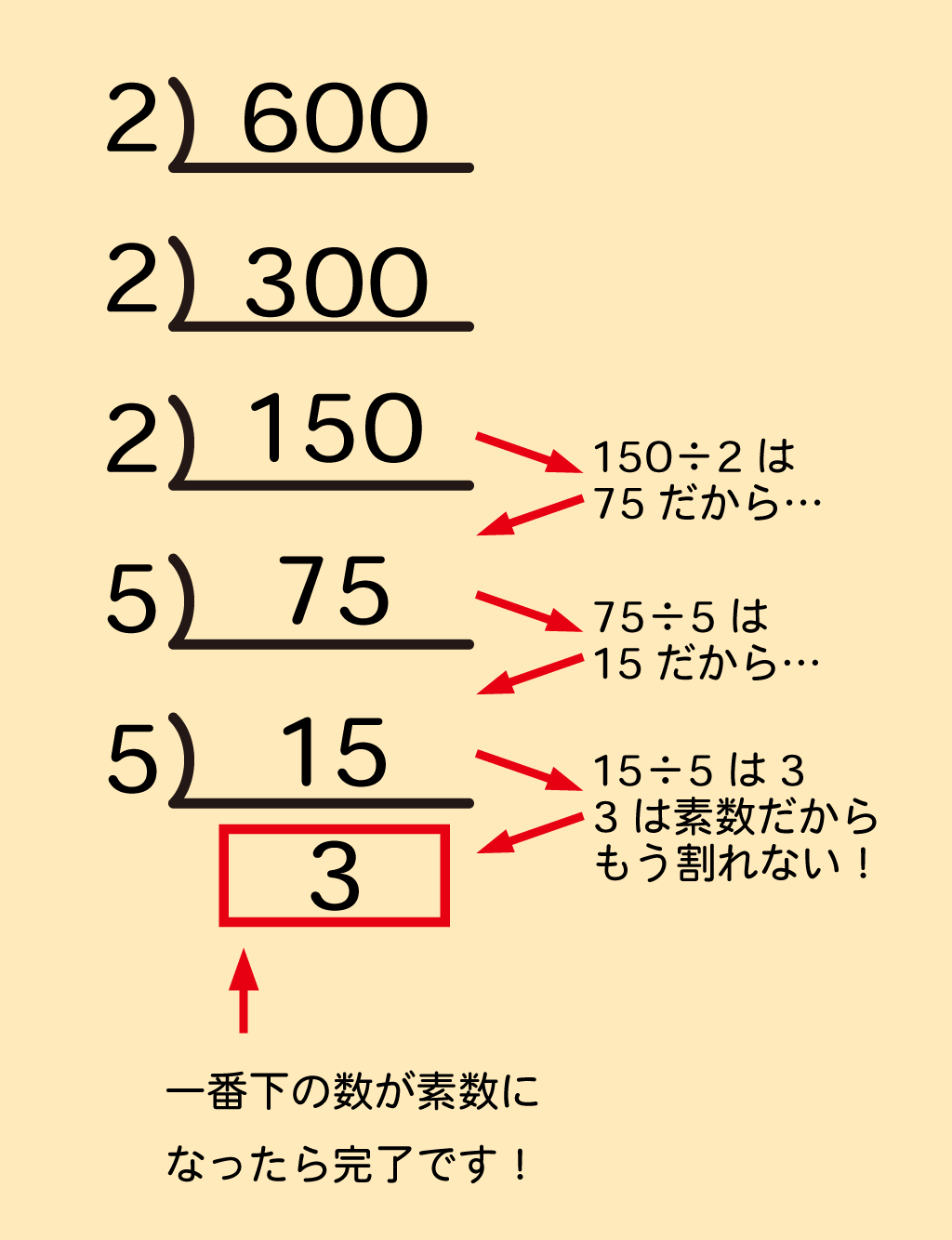平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	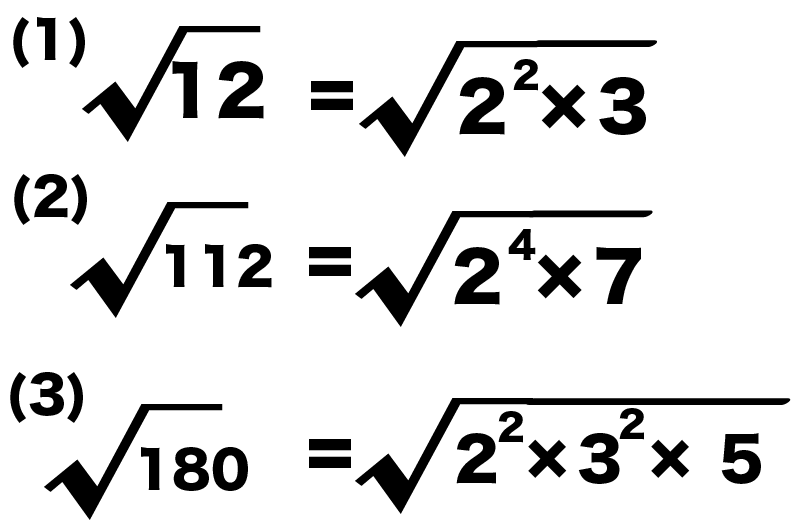平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者
平方根の活用 式の値と近似値の求め方 教遊者	平方根の活用 式の値と近似値の求め方 教遊者

以上、因数分解を利用した2次方程式の解き方でした。 今回のように「\(x(x )=0\)」や「\((x )(x )=0\)」というようにきれいに因数分解できる場合はこの方法で解くことができます。 ただし、2次方程式の中にはきれいに因数分解できない場合もあります。今回は、難関高校の入試に出題された因数分解の難問を解説していきます。 因数分解は、必ず取りたい問題の1つです。 実際に出題された問題から抜粋して紹介しているので これらの問題を全部解けるようになれば、本番もバッチリのはず！